Task Parallelization

Task parallelization is a method to spread the computing workload on the many cores of a computer. Instead of splitting the data accross cores and apply the same task to all these pieces, different tasks are split accross the cores with the data necessary to complete them. This approach can often make the computation faster, especially with non-uniform plasma distributions.

Task parallelization of macro-particle operations in Smilei (using OpenMP) is published in [Massimo2022].

Motivation

Usually, most of the computing time is spent on macro-particle operations. Consequently, a non-uniform plasma distribution results in load imbalance: some cpu cores are loaded with less macro-particles, and idly wait for the other cores to finish their work.

Worse: adding more cpu cores will not result in significant speedup, as only a few of them are performing most of the work. This “strong scaling” curve (speed-up vs number of cpu-cores) starts to saturate. Several methods for parallelism can increase the number of computing units where the saturation occurs.

In Smilei, by default, the data is split in patches (see Parallelization basics) and, when the environment variable OMP_SCHEDULE is set to dynamic, the OpenMP scheduler dynamically assigns each patch to each core. This provides for some load balancing inside each MPI process, as cores can work asynchronously on different patches.

This strategy implies that only 1 OpenMP thread can work on a given patch, which includes potentially several Species and all the PIC operators (interpolation, push, etc). These constraints can considerably slow down the simulation in some situations (many species with non-uniform distribution, and/or low number of patches per core).

A first solution is to split the data to a finer level: separate the treatment of species, and split the patch in smaller structures (in Smilei, patches are divided in clusters along the dimension x). This can improve the strong scaling results, but some constructs cannot be parallelized with this data splitting (e.g. irregularly nested loops, recursion, etc). The task parallelism has been introduced to answer these issues.

Task approach

Smilei exploits the task parallelization (including task dependencies) available with OpenMP 4.5. The main idea is to split the work in smaller units that can be run asynchronously, respecting the logical order in which these units of work must be completed.

In addition to separated species treatment and patches split in clusters (see cluster_width and the following Figure), the macro-particle operators (interpolation, push, etc) are defined as tasks. All the combinations of [operator-cluster-species-patch] correspond to different tasks that can be run in parallel.

../_images/Cluster_definition_doc.png

Fig. 70 Definition of clusters in a patch. The depicted 2D patch’s size is 16 × 6 cells in the x and y directions respectively. In the Figure each cluster has an x extension equal to cluster_width = 4 cells in the x direction.

Task dependency graph

Some tasks logically depend on other tasks, e.g. the position and momenta of the macro-particles of a certain [cluster-species-patch] combination can be advanced in a given iteration only after that the electromagnetic force acting on them in that iteration has been interpolated from the grid.

The combinations [operator-cluster-species-patch] are defined as tasks, with dependencies respecting the PIC macro-particle operator sequence (Interpolation, Push, Projection) on the respective [cluster-species-patch] combinations.

In task programming, the task dependencies of an algorithm are represented by a task dependency graph, where each task is a node of the graph and the directed edges between nodes are the task dependencies. If in this graph an arrow spawns from task A to task B, then task B logically depends on task A.

In the code, the dependency graph is provided to OpenMP in form of depend clauses in the omp task directives. This way, the tasks are dynamically assigned to OpenMP threads, in the correct order (preventing data race conditions). The user does not have to worry about the assignment of tasks to the available threads, as this operation is done dynamically by the OpenMP scheduler.

This is described in [Massimo2022].

Performance Results

Some results from [Massimo2022] are shown in the following.

In the following Figure, a 2D uniform thermal plasma case shows that with uniform macro-particle distributions the task-parallelization in Smilei does not have a performance advantage. In the same Figure, a 2D radiation pressure acceleration case shows that task parallelization can have a performance advantage with non-uniform macro-particle distributions.

../_images/Cluster_width_scan_doc.png

Fig. 71 Performances with and without task parallelization in a 2D uniform plasma case (left) and in a 2D radiation pressure acceleration case (right).

Note in the following Figure the non-uniformity of the electrons distribution in the radiation pressure acceleration case. The non-uniformity is present since the start of the simulation. A namelist for a similar case can be found in the benchmarks/tst2d_02_radiation_pressure_acc.

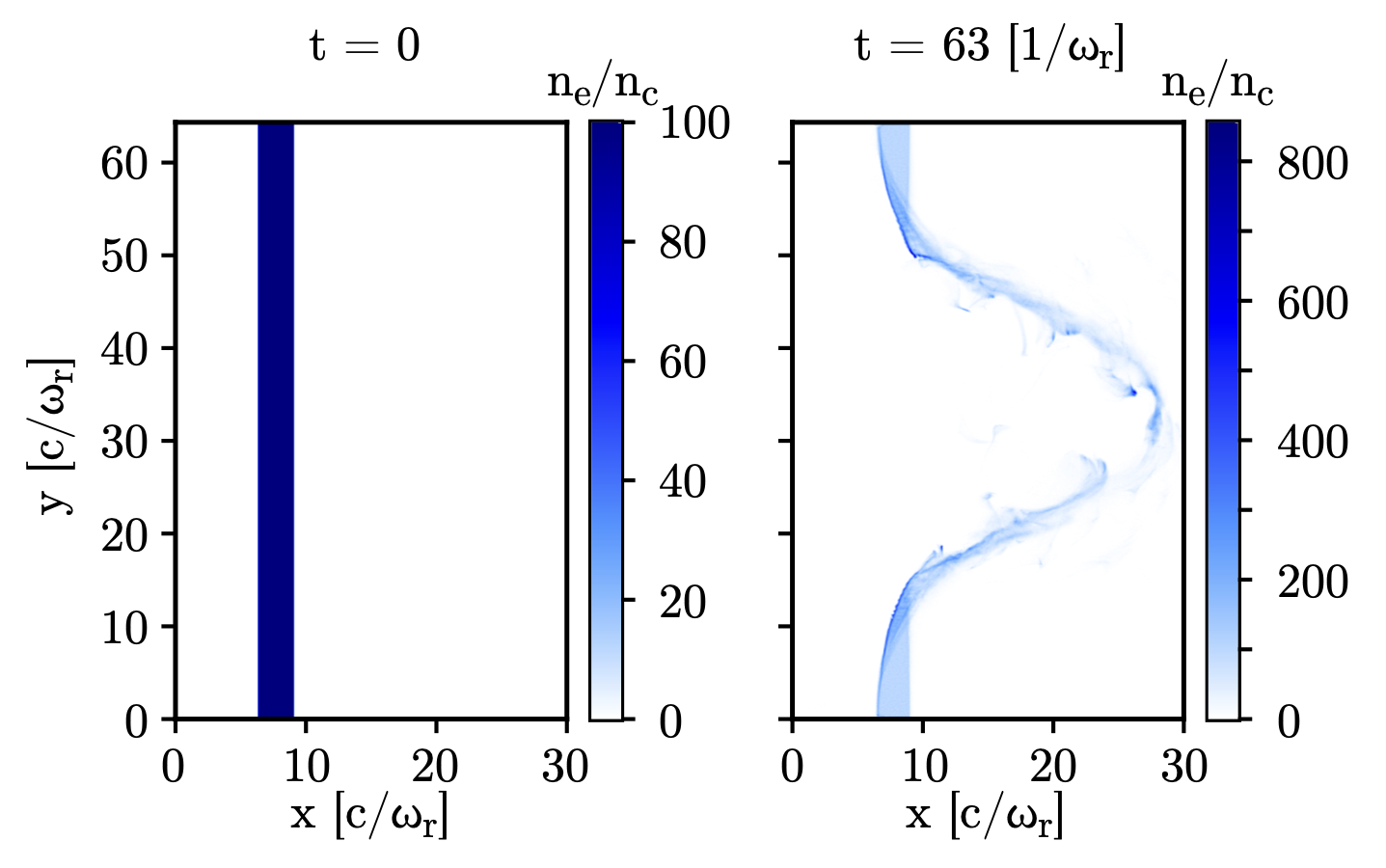
../_images/Radiation_Pressure_Rho.png

Fig. 72 Electron density divided by the critical density in a 2D radiation pressure benchmark at 0 (left) and 1500 iterations (right). The non-uniformity of the macro-particle distribution is present since the start of the simulation.

The scheduling of macro-particle operations without and with task parallelization can be seen in the following figures. Note how in the first Figure (without task parallelization), the end of the treatment of macro-particle operators (around 0.1 s) is determined by the OpenMP thread 0 of the MPI process 0. In the second Figure (with task parallelization), the OpemMP thread 2 of MPI process 0 determines the end of the treatment of macro-particle operators (around 0.07 s). In this case, the finer decomposition given by the clusters and the relaxation of the constraints involved in the assignment of macro-particle operations to threads yields a shorter time to the result.

../_images/Task_tracing_doc.png

Fig. 73 Scheduling of macro-particle operations for the 2D radiation pressure benchmark, 4 MPI processes and 4 OpenMP threads, during iteration 1200, without (left panel) and with task parallelization, 4 clusters per patch (right panel).