Exercises¶
Exploring the input namelist¶
To run a simulation, you need to specify the phenomena it will describe and
the numerical parameters to study your case, e.g. the resolution, the integration timestep, the grid size,
in an input file, in this case called InputNamelist.
In the next few exercises we will understand the basic set-up of a simulation described this file.
One of the first variables we define in this simulation is the lambda0, i.e. the laser carrier frequency
\(\lambda_0\).
Exercise 1
Assuming \(\lambda_0=0.8 \mu m\) (a Ti:Sa laser system), what is the value of the critical density \(n_c\)?
What is the value of the reference electric field \(E_0=(2\pi m_e c^2)/(e\lambda_0)\)?
This choice of \(\lambda_0\) will be used throughout all subsequent exercises.
Hint: Some lines at the start of the InputNamelist.py file can help you in the calculations.
The InputNamelist.py file starts with the definition of physical constants and units,
mesh points, integration timestep, etc.
Some of these parameters are inserted in the first block of the simulation, called Main block.
Others may be useful for conversions between units or to define other variables in the file.
In the Main block, you also find the geometry of the simulation, which is AMcylindrical.
The grid is defined on a cylindrical space and with cylindrical coordinates x, r, but the particles move in the 3D space
x, y, z (See Fig. 1).
In the simulations of this practical work, Maxwell’s equations are solved in
cylindrical coordinates with cylindrical symmetry, which allows for quick
simulations with 3D accuracy.
Note a block called MovingWindow in the InputNamelist.py.
In the physical case being considered, a laser pulse with duration of tens
of femtoseconds propagating along the positive x direction is simulated.
We are only interested in phenomena near the laser pulse
(within tens of microns), like plasma wave excitation, so a Moving Window is defined,
which emulates a camera moving at the speed
we want, along the positive x direction.
In this physical case, the moving window speed is set to c to follow the laser. As a result,
the laser pulse is almost immobile in the simulation window.
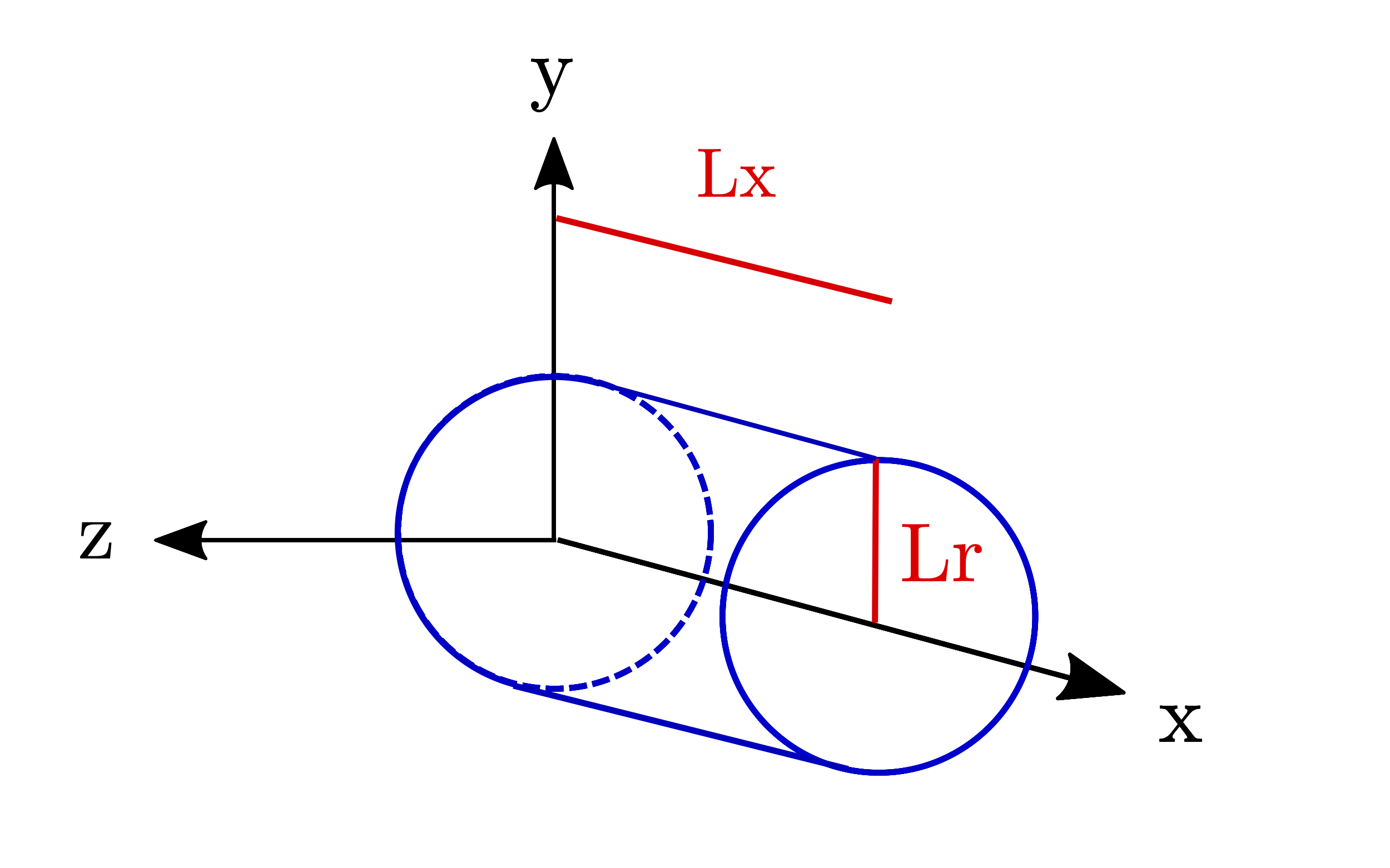
Fig. 1 Reference axes of the simulation. The simulation window corresponds to the cylinder with radius Lr and length Lx.¶
Fig. 2 Simulation set-up at the start of the simulation in this Section (not to scale)¶
Exercise 2
What are the longitudinal size Lx and radial size Lr of the simulation window?
How many mesh points nx and nr are used in the longitudinal and radial directions?
What is the resolution dx and dr in the longitudinal and radial directions?
See Figures 1 and, 2 for reference, and find these lengths in the InputNamelist.py.
At the end of the InputNamelist.py file,
there are blocks starting with the word Diag.
These blocks are for the diagnostics/outputs of the code.
The first Diag is a DiagProbe defined on a line
(so a 1D diagnostic), on the propagation axis of the laser (the x axis).
This diagnostic returns the value of some physical fields
along that axis. We call this probe Probe0 (the 0 because
it is the first Probe in the namelist). The second diagnostic block is
a DiagProbe defined on the plane xy (so a 2D diagnostic).
This is the second probe of the namelist, so it is called Probe1 (Python starts counting from zero.)
Laser pulse in vacuum¶
Everything is ready to run your first simulation.
We will start adding a laser pulse propagating in vacuum, along the positive x direction.
Action in the InputNamelist.py file, uncomment the lines
with the laser pulse parameters and the LaserEnvelopeGaussian block.
Afterwards, launch the simulation with sbatch submission_script.sh.
This block defines a laser pulse in the simulation with a transverse field based on the definition of a Gaussian Beam [Siegman], with a carrier wavelength \(\lambda_0=0.8 \mu m\).
Furthermore, the considered pulse is modulated with Gaussian temporal profile, whose FWHM length is much larger than the laser carrier wavelength \(\lambda_0\), defined in the variable lambda0 (see Fig. 3).
The laser transverse electric field is linearly polarized in the y direction.
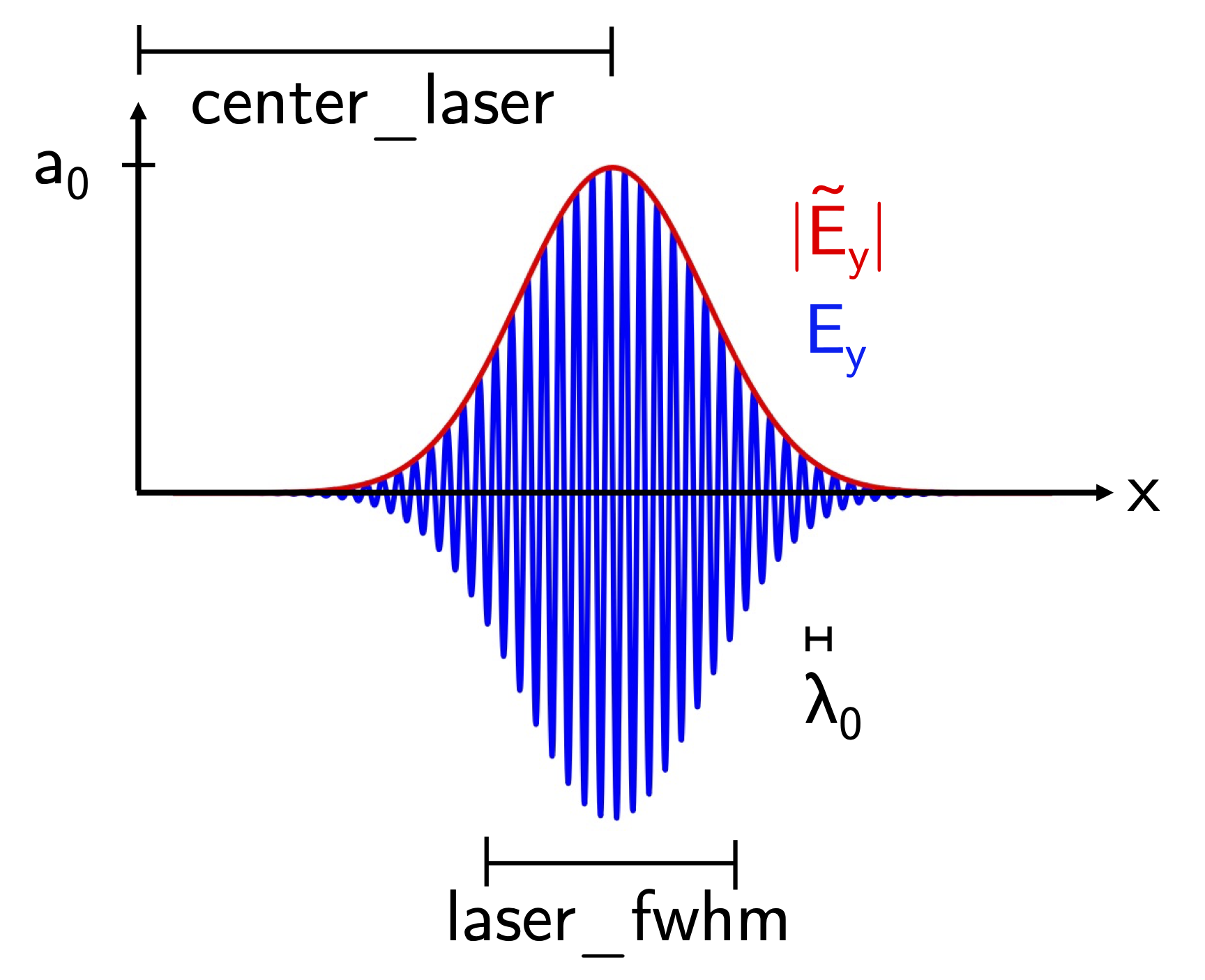
Fig. 3 Definition of the laser parameters (not to scale). In blue, the normalized transverse electric field of the laser, in red the absolute value of its complex envelope. All quantities are in normalized units (e.g. \(\lambda_0/2\pi\) for the lengths, \(m_e\omega_0c/e\) for the fields).¶
The simulation now includes a moving window and a laser pulse, as in Fig. 4.
Fig. 4 Simulation set-up at the start of the simulation(s) in this Section (not to scale).¶
Note: an envelope model is used to describe the laser pulse, as described in [Massimo].
Therefore, the laser field and the electromagnetic fields it will excite in the plasma
will not show the high frequency oscillations.
The envelope of the laser transverse electric field is contained in the field Env_E_abs.
Exercise 3
Find the laser pulse parameters in the InputNamelist.py.
What are the waist size, FWHM duration in field, and FWHM duration in intensity of the laser pulse?
In the simulation window, where is placed the center of the laser pulse at the start of the simulation?
Where is the focal plane of the laser pulse localized?
Exercise 4
The normalized laser peak field is given by \(a_0 = eE/m_e\omega_0c\), where \(E\) is the laser electric field peak and \(\omega_0 = 2\pi c/\lambda_0\) is the laser central frequency (\(\lambda_0 = 0.8 \mu m\).)
Using the laser \(a_0\) set in the namelist for the calculations, what is the laser peak intensity \(I = c\varepsilon_0 |E|^2\) of the laser pulse?
Hint: the input namelist contains the physical quantities that you may need for the conversions.
Action When the simulation is completed (the word END should appear in the log file), open IPython with the command ipython.
Then, you can check the initial position of the laser through the commands:
import happi; S = happi.Open()
S.Probe.Probe0("Env_E_abs",units=["um","fs","TV/m"],timesteps=0).plot( figure=1, xlabel="x [um]")
S.Probe.Probe1("Env_E_abs",units=["um","fs","TV/m"],timesteps=0).plot( figure=2, xlabel="x [um]",ylabel="y [um]")
Probe0 is a 1D diagnostic defined on the laser propagation axis, while Probe1 is a
2D diagnostic defined on the plane \(xy\). Note that in the commands we have specified
timesteps=0 to see the laser pulse at the start of the simulation.
Check that the initial laser position that you are seeing is the same specified in the input namelist. Remember that the laser pulse is modeled through its envelope, so you can not see its high frequency oscillations with wavelength \(\lambda_0\).
We can study the laser diffraction in vacuum. To see the evolution of the laser, use:
S.Probe.Probe1("Env_E_abs",units=["um","fs","TV/m"]).slide( figure=3, xlabel="x [um]",ylabel="y [um]" )
You can move the horizontal time bar to see the snapshots at different iterations. Note that the Moving Window makes the laser seem immobile in the simulation, but it is moving at speed c, and the Moving Window is following it with the same speed.
If you do not specify a vmax value (the colorbar maximum) in the previous command,
happi will change it at each iteration. To better see the laser diffraction,
try to specify a colormap maximum with vmax. For example:
S.Probe.Probe1("Env_E_abs",units=["um","fs","TV/m"]).slide( figure=3,vmax=0.3, xlabel="x [um]",ylabel="y [um]" )
Exercise 5
In the next exercise we will check that the Gaussian laser pulse diffracts following the theory for a Gaussian beam [Siegman]: \(w(x) = w_0\sqrt{1 + x^2/x^2_R }\), where \(w_0\) is the laser waist size at the focal plane position, \(w(x)\) the laser waist size at propagation distance \(x\), \(x_R\) is the Rayleigh length \(x_R = \pi w_0^2/\lambda_0\).
What is the theoretical Rayleigh length \(x_R\)?
Exercise 6
Use the script Laser_waist_theory_vs_Smilei.py to compare the analytical diffraction law of the previous exercise and the your Particle-in-Cell (PIC) simulations results. Copy the script in the simulation folder or call the script from that folder. The script loads the results, then loops over the iterations available in output and computes the laser pulse waist \(w(x)\) as
After this calculation, the simulated waist is compared to the corresponding analytical value.
Run the script (from IPython use %run Laser_waist_theory_vs_Smilei.py)
to plot the comparison and include the image in your answers.
Laser wakefield excitation¶
Now we will add a preionized hydrogen plasma to excite plasma waves in the wake of the laser pulse. The laser pulse is considered intense enough to assume that the hydrogen gas was already ionized, much before the arrival of the laser pulse peak (see the laser intensity computed in Exercise 3).
Action Uncomment the first Species block, the related variable definitions and
take some time to read them carefully.
This block defines a particle Species
in the simulation, whose name is plasmaelectrons. Note the normalized mass
and normalized charge of these particles defined in this block (1.0 and -1.0 respectively).
Since the normalizing mass and charge are the electron mass and the unit charge,
we know that these particles are electrons.
After a short linear ramp, the plasma density profile
is uniform for one millimetre in the x direction and within a distance Radius_plasma=30 \(μm\)
from the laser's propagation axis.
Therefore, now the simulation includes a moving window, a laser pulse (modeled by its envelope) and electron plasma, as represented in Fig. 5.
Fig. 5 Simulation Setup at the start of the simulation(s) in this Section (not to scale).¶
Exercise 7
As you can see, the plasma density has a value \(n_0 = 1.\cdot10^{18} electrons/cm^{3}\).
What is the ratio between the plasma density and the critical density (computed for Exercise 1)?
Is it an underdense or overdense plasma?
As we did with in Exercise 6 for the laser pulse in vacuum,
the first step is to verify that the plasma behaves as predicted by
the analytical theory. If we reduce the laser pulse a0 to 0.01,
the laser pulse satisfy the conditions for the applicability of the
1D linear theory of plasma wave excitation.
Exercise 8
The analytical 1D linear theory (which can be applied in our case for \(a_0 \ll 1\)) predicts the formation of a sinusoidal wave at plasma frequency \(\omega_p^2 = e^2n_0/m_e\varepsilon_0\) behind the laser, where \(n_0\) is the plasma density.
Action Launch the simulation with \(a_0 = 0.01\) (you will need to change this variable in the InputNamelist.py).
Study the evolution of the electric field Ex with the diagnostics Probe0 and Probe1.
You can use the same plot commands of the previous section, but applied to Ex instead of Env_E_abs,
for example with
import happi; S=happi.Open()
S.Probe.Probe0("Ex",units=["um","fs","GV/m"]).slide( figure=3, xlabel="x [um]" );
S.Probe.Probe1("Ex",units=["um","fs","GV/m"]).slide( figure=3, xlabel="x [um]",ylabel="y [um]" )
What is the theoretical plasma wavelength \(\lambda_p = 2\pi c/\omega_p\)?
What is the plasma wavelength that can be estimated from the simulation results?
Note an estimate inferred from the plot is sufficient for the purposes of this practical.
Exercise 9
The longitudinal electric field on the axis of this linear plasma wave, according to the 1D linear theory [Esarey2009] applied to the considered case, is given by (in physical units):
Action Use the script Ex_linear_theory_vs_Smilei.py
to compare the analytical result given by Eq. (2) and
the simulated results (%run Ex_linear_theory_vs_Smilei.py on IPython).
Again, you will need to copy the script in the simulation folder or to call it from there.
Does the simulation agree with theory? Include the image in your answers.
Considering the laser and plasma quantities in the namelist, when \(a_0 \ll 1\), the excited plasma wave is in the (laser-plasma) linear regime of interaction. As we saw in Exercise 8 and Exercise 9, in the linear regime the plasma wave in the wake of the laser has sinusoidal shape. Increasing \(a_0\), the laser becomes more intense. When \(a_0 \gtrsim 1\) the plasma electrons begin to reach relativistic velocities. At this limit, the electron inertia increases, elongating the plasma period and wavelength, resulting in electron accumulation at the end of each wave period. Moreover, increasing \(a_0\), the longitudinal electric field waveform changes from a sinusoid to a sawtooth wave [Esarey2009]. In this regime of interest for plasma acceleration, PIC simulations become necessary since there are no longer general analytical solutions to the coupled Vlasov-Maxwell system of equations, and fluid theory cannot be applied.
Exercise 10
Launch a new simulation with a0=2.3, i.e. its original value.
This simulation will be in the nonlinear regime (\(a_0>1\)), so the plasma wave will not be sinusoidal.
You can visualize both the normalized absolute value of the envelope of the laser field and the electron number density by defining a transparency
for the parts where the latter field is lower than a threshold vmin:
import happi; S=happi.Open()
Env_E = S.Probe.Probe1("Env_E_abs",units=["um","fs"],cmap="hot",vmin=0.8,transparent="under",pad=0.5)
Rho = S.Probe.Probe1("-Rho/e",units=["fs","um","1/cm^3"],cmap="Blues_r",vmin=0.,vmax=3e18)
happi.multiSlide(Rho,Env_E,xmin=0,figure=10, xlabel="x [um]",ylabel="y [um]")
Using timesteps=2500 in the definition of Env_E and Rho, and then using multiPlot instead of multiSlide,
you should have a plot of the data at half of the propagation length.
Include this image in your answers.
Action Create three folders, sim1, sim2, sim3, where you will launch the simulation with
\(a_0 = 0.5, 1.4, 2.0\) respectively. Take a look at the longitudinal electric
field on axis (Probe0) and to the 2D plasma density (Probe1):
import happi; S=happi.Open()
S.Probe.Probe0("Ex",units=["um","fs","GV/m"]).slide( figure=1,xlabel="x [um]" )
S.Probe.Probe1("-Rho/e",units=["um","fs","1/cm^3"]).slide( figure=2,xlabel="x [um]",ylabel="y [um]" )
Note In some cases you may need to add suitable vmin and vmax values for the plot command. In the linear regime of interaction, probably you will not see any oscillation
in the plasma density, but still, you can see oscilations on the electric field Ex.
In the nonlinear regime of interaction (higher \(a_0\)), you need to reduce the vmax
in the plot/animate command to see the formation of the wake. This happens because, at the end
of the plasma wave period, there is an accumulation of electrons,
which hides the other charge density values.
Exercise 11
Check that the simulations in the three folders sim1, sim2, sim3,
with respectively \(a_0 = 0.5, 1.4, 2.0\), are completed.
We will compare the longitudinal electric field Ex
of these three simulations to see how the wave profile changes when increasing \(a_0\).
With happi you can easily do it:
import happi
S1=happi.Open("path/to/sim1")
Ex1=S1.Probe.Probe0("Ex",units=["um","fs","GV/m"],timesteps=1000,label="a0 = 0.5")
S2=happi.Open("path/to/sim2")
Ex2=S2.Probe.Probe0("Ex",units=["um","fs","GV/m"],timesteps=1000,label="a0 = 1.4")
S3=happi.Open("path/to/sim3")
Ex3=S3.Probe.Probe0("Ex",units=["um","fs","GV/m"],timesteps=1000,label="a0 = 2.0")
happi.multiPlot(Ex1,Ex2,Ex3,figure=3,xlabel="x [um]")
Remember to substitute the real path of your simulations in the Open command.
The command multiPlot is used to superpose multiple lines in the same plot window.
This command is also used in some of the exercises of the following section.
Include the resulting image of the command above in your answers.
In another plot window, adapt the last commands to plot the plasma number density -Rho/e (with units=["um","fs","1/cm^3"]) from the three simulations.
Include also this image in your answers.
Include a plot of the period of the plasma wave as function of the a0 of the laser pulse.
You should see the plasma wavelength relativistically elongated with a more intense laser pulse.
Hint: You may estimate as the distance between two consecutives zeros in the Ex field on the propagation axis.
Behind the curtain: Why are ions not present? A plasma for laser wakefield acceleration is normally made of ions and electrons at least, so why are ions not present in this namelist? The answer can be found in the properties of Maxwell’s Equations and implies some derivations. For the moment it is sufficient to say that, since we set to zero the plasma electromagnetic field at the beginning of these simulations, and that we solve carefully Maxwell’s Equations and the particles equations of motion; then, defining the plasma made of electrons will make the code behave as if there is also a neutralizing layer of immobile ions. Since ions do not move in the timescales of interest for the phenomena we are simulating (their mass is ~1840 times larger than the electron mass), this is a reasonable approximation that, in addition, removes the need to simulate the ions, what brings a significant computational gain. The complete answer for the interested reader can be found in the dedicated section of this tutorial.
Laser wakefield acceleration of an electron bunch¶
We are ready to simulate a basic laser wakefield accelerator for electrons. Just as a surfer rides the waves in the water, an electron bunch can be accelerated by plasma waves. Remember, an immobile surfer will not be accelerated by a wave. To effectively interact with the wave, the surfer must first paddle to acquire some velocity. If the surfer moves near the speed of the wave, an accelerating phase of the wave will be experienced by the surfer for a significant portion of the surfer-wave interaction.
Following the same analogy, to be accelerated, the electrons must be injected in the accelerated phase of the plasma wave with a speed near the wave's velocity (approximately the speed of light). Many clever injection schemes have been investigated since the 2000s, such as those described in [Esarey2009], [Malka2012], [FaureCAS] , where the electrons of the plasma itself are in some way injected into the laser-driven wave.
As already mentioned, in this practical work we will study an external injection scheme, in which a relativistic electron bunch is injected from outside the plasma. This will allow us to understand the basic concepts of electron injection in a plasma wave, even though it is challenging to achieve experimentally.
Action In a new simulation folder, set again the \(a_0\) of the laser to the value \(2.3\)
Uncomment the two Species blocks, the related variable definitions and
take some time to read them carefully. To track the evolution of the electron bunch during its propagation,
you will have to uncomment also the DiagTrackParticles block. Afterwards, you can launch the simulation.
As you can see, the second Species block defines a Species
called electronbunch, which we will inject in the plasma wave for acceleration.
As for the Species called plasmaelectrons of the previous Sections,
these particles have normalized charge and mass equal to -1.0 and 1.0 respectively,
thus they are electrons. In the present case, the plasma density is not defined through a
density profile function, but the coordinates and momenta of each of the bunch’s macro-particles
are given to the code through arrays. The variable npart defines the number of macro-particles of the bunch (in this case 50000).
In our case, these coordinates
and momenta are generated to initialize a relativistic electron bunch with Gaussian charge density distribution.
The electron bunch dimensions are defined through its rms size on the various axes,
Note For your future simulation work, this initialization method can be used also to use a macro-particle distribution obtained from another code (a magnetic transport code for conventional accelerators for example). Instead of generating randomly the particles coordinates and momenta, you only need to read them with Python.
The simulation now includes a moving window, a laser pulse (modeled with its envelope), plasma electrons and an electron bunch, as in Fig. 6.
Fig. 6 Simulation Setup at the start of the simulation(s) in this Section (not to scale).¶
Exercise 12
Reading the namelist, provide a description of the electron bunch at t = 0.
What is the total charge, the energy, the rms sizes along x, y, z, the rms energy spread, and the normalized emittance along the transverse planes?
Where is the electron bunch placed in relation to the simulation window at the instant of time t = 0?
As the name suggests, this diagnostic block allows to track particles,
specified by their species name and some filter. Using a filter
(e.g., selecting only the particles with energy higher than 50 MeV) is
particularly useful when you have many particles in a Species,
like in the plasma of the namelist. In that case, not using a filter
would make this diagnostic computationally heavy and would store
the coordinates of too many particles. In the case of the bunch,
there is no need to specify a filter, since the number of macro-particles
is sufficiently small to be manageable. As you can see from the namelist,
in this diagnostic, we store the coordinates and momenta of the particles,
as well as their weight (from which their charge can be computed).
Exercise 13
Check that the simulation with the electron bunch has ended. This time the simulation will run a little longer.
Plot the 2D charge density (use Probe1) at timesteps=3000 and timesteps=5000
and play with the parameter vmax to be able to see the electron bunch
in the plasma wave.
Include these images in your answers.
Exercise 14
With the same simulation of Exercise 13, use the command
happi.multiPlot to plot in the same window
the longitudinal electric field Ex and the number density Rho/e
from Probe0 (1D diagnostic) at timesteps=3000 and timesteps=5000.
You may need to rescale the quantities (see Postprocessing).
Playing with multiplying factors in the plot you should be able
to clearly see where the electron bunch is placed in the plasma wave.
Include these images in your answers.
Exercise 15
With the same simulation of Exercise 12, run the script Compute_bunch_parameters.py in the simulation folder to read the electron bunch parameters.
For this purpose, from IPython you can use the command %run Compute_bunch_parameters.py timestep,
where timestep is the timestep you are interested in.
For example, the command %run Compute_bunch_parameters.py 5000 will return the electron bunch parameters the end of the simulation (i.e, at timestep = 5000).
What is the energy gain \(\Delta E\) you measure from the start (timestep = 0)
to the end of the simulation (timestep = 5000)?
What is the simulated propagation distance \(L\)?
From this information, estimate the average accelerating field \(E_{acc}\), including the details of your calculation.
What is the absolute and relative rms energy spread at the beginning and at the end of the simulation?
Report all the electron bunch parameters at the start and at the end of the simulation.
Exercise 16
With the same simulation of Exercise 13, use the script Follow_electron_bunch_evolution.py to see how the bunch has evolved during
the simulation (%run Follow_electron_bunch_evolution.py
in IPython). The script reads the DiagTrackParticles output and
then computes some bunch quantities (rms size, emittance, energy)
at each available output iteration.
Include the resulting image in your answers.
From the evolution of the bunch energy, can you estimate the average accelerating field?
Compare this value to the one computed in Exercise 14.
Exercise 17
Create four new folders, sim1, sim2, sim3, sim4
where you will run four new simulation. In each simulation, the charge of the electron bunch will be changed to \(20, 40, 60, 100 pC\), respectively.
Warning: Do not forget the minus sign or the bunch will be made of positrons!
Adapt the commands you have used in Exercise 10 (happi.multiPlot commands) to plot the longitudinal electric
field Ex for the four cases. i) What do you observe? Include this plot in the answers.
Use the script
Compute_bunch_parameters.py
used for Exercise 14 to find the energy gain of the
electron bunch at timestep 5000 for each one of the four cases.
Can you explain how the deformation of the Ex waveform results in different final energies?
Hint: You can compare the Ex of the four simulations with multiPlot.
Include a plot of the energy gain of the bunch obtained for charges \(40, 60, 80, 100 pC\). You can use Python or any other language for this simple plot. For example, using Python:
import matplotlib.pyplot as plt
bunch=[20,40,60,100]
energy=[...,...,...,...] #replace by the energy values you obtained
fig = plt.figure()
plt.plot(bunch, energy, 'ro', markersize=10)
plt.xlabel(' Bunch charge [pC] ')
plt.ylabel(' ... ')
plt.show()
Exercise 18
Create other four folders, sim5, sim6, sim7, sim8,
where you will launch the simulation varying the bunch distance from the laser, changing the delay_behind_laser parameter (Set again the charge to \(60 pC\) for all these simulations).
This parameter controls the distance between the electron bunch and the laser center, therefore its phase in the plasma wave behind the laser pulse.
For delay_behind_laser, try the values \(20, 22, 24, 26. \mu m\).
What is the observed final energy for each of the four delay_behind_laser parameters?
Using happi.multiPlot (see Exercise 10), plot the longitudinal electric field Ex for the four simulations (show all curves in the same window and include the final image in your answers).
Again using happi.multiPlot, plot the electron number density Rho/e for the four simulations (show all curves in the same window and include the final image in your answers).
Include a plot with the delay_behind_laser on the horizontal axis and the energy gain on the vertical axis. You can use Python or any other language
for this simple plot (as you did for Exercise 16)
Exercise 19
For the same simulation of Exercise 13, using the TrackParticles diagnostic
and Probe diagnostic, write a script that takes as input variable, an iteration number i.e., timestep.
The script should plot in the same panel the longitudinal electric field Ex along the propagation axis x and a scatter plot of the electron bunch phase space x and px
to show the particles’ positions in the accelerating phase of Ex in that iteration.
The plot should report the correct units and labels in the axes.
In your answers, include the script and the output image using timesteps=3000 and timesteps=5000.
function using only dot markers.
Hint 1: To extract the propagation axis (in \(\mu m\)) and the Ex field (in GV/m) at the required timestep, you can use:
import happi
import numpy as np
S=happi.Open()
# in GV/m
Ex=np.asarray(S.Probe.Probe0("Ex",timesteps=timestep,units=["um","GV/m"]).getData())[0]
moving_x=np.linspace(0,S.namelist.Lx,num=S.namelist.nx)*S.namelist.c_over_omega0*1e6
x_window_shift = S.Probe.Probe0("Ex").getXmoved(timestep)*S.namelist.c_over_omega0*1e6
# in um
propagation_axis = moving_x + x_window_shift
Hint 2: To export the x (in \(\mu m\)) and px (in MeV/c) of the bunch macro-particles, you can use:
track_part = S.TrackParticles(species ="electronbunch",axes = ["x","px"],timesteps=timestep)
# in um
x_bunch=track_part.getData()["x"]*S.namelist.c_over_omega0*1e6
# in MeV/c
px_bunch=track_part.getData()["px"]
Hint 3: The Ex and px will have very different scales, so you will need
to use two y axes with different scales to see something meaningful.
With matplotlib you can do it through twinx.
Hint 4: Use a scatter plot for the x and px data of the bunch. For the propagation_axis and Ex plot, use a simple plot command.
Exercise 20
The accelerated electron bunch macro-particles do not have the same energies, so it is interesting to see the energy distribution or energy spectrum of the bunch particles before and after the acceleration.
Write a Python script to read the output of the DiagTrackParticles, and then use it to draw the energy spectrum (i.e. a histogram of the bunch macro-particle energies)
of the electron bunch (using MeV for the energies on the horizontal axis).
Provide the script and figures of the energy spectrum at timesteps 0 and 5000 (the start and the end of the simulation).
The horizontal axis should be in MeV, while the vertical axis should be in pC/MeV.
Verify that the sum of the histogram bins is equal to the bunch charge and include also the
corrects units and labels in the plot.
Briefly comment on the differences in the energy spectrum at the start and at the end of the simulation.
Hint 1: You can extract the energy and charge of each macro-particle of the bunch at the desired timestep, using:
import happi
import numpy as np
import scipy.constants
import math
import matplotlib.pyplot as plt
S=happi.Open()
# Constants
c = scipy.constants.c # lightspeed in vacuum, m/s
epsilon0 = scipy.constants.epsilon_0 # vacuum permittivity, Farad/m
me = scipy.constants.m_e # electron mass, kg
q = scipy.constants.e # electron charge, C
electron_mass_MeV = scipy.constants.physical_constants["electron mass energy equivalent in MeV"][0]
lambda0 = S.namelist.lambda0 # laser central wavelength, m
conversion_factor_length= lambda0/2./math.pi*1.e6 # from c/omega0 to um, corresponds to laser wavelength 0.8 um
nc = epsilon0*me/q/q*(2.*math.pi/lambda0*c)**2 # critical density in m^(-3)
# extract data from TrackParticles
track_part = S.TrackParticles(species ="electronbunch",axes = ["w","px","py","pz"],timesteps=timestep)
# extract charge in pC
conversion_factor_charge= q * nc * (conversion_factor_length*1e-6)**3 * 10**(12)
charge_bunch_pC=track_part.getData()["w"]*conversion_factor_charge
# extract momenta in MeV/c
px_bunch=track_part.getData()["px"]
py_bunch=track_part.getData()["py"]
pz_bunch=track_part.getData()["pz"]
p_bunch = np.sqrt((px_bunch**2+py_bunch**2+pz_bunch**2))
# electron energy in MeV
E_bunch = np.sqrt((1.+p_bunch**2))*electron_mass_MeV
Hint 2: you can use the matplotlib function numpy.histogram to compute a
histogram of the macro-particles energies and the bins/edges of the horizontal axis.
The energy spectrum is a histogram of the macro-particle energies using their charge as statistical weight.